a* algorithm for pathfinding

One of the topics we covered about AI in the course CS380 taught by Iker Silvano was pathfinding, which I found really interesting.

For one of the assignments, a C++ solo project, we had to implement an efficient A* algorithm.

General characteristics

The combination of Best-First and Dijkstra algorithms has become one of the most popular choices for pathfinding, the A* algorithm.

It is considered a complete algorithm, meaning that it will always eventually find a solution to the problem if a solution exists.

It is a heuristic search algorithm as it uses a search strategy that attempts to optimize a problem by iteratively improving the solution based on a given heuristic function or a cost.

Best-First

Best-first search is a search algorithm which explores a graph by expanding the most promising node chosen according to an heuristic function.

Dijkstra

Dijkstra’s algorithm finds the shortest paths to a graph’s vertices in order of
their distance from a given source.

You can find tons of sites throughout the internet that explain the algorithm in depth.

About the demo

The video above is a showcase of the A* algorithm demo, in which apart from the actual implementation of such algorithm, I implemented several other features:

Straight line optimization
Rubber banding
Smoothing
Multiple heuristic computation functions (euclidean, octile, chebyshev and manhattan)
A variable weight for the cost of each node
Ability to divide the computation of the A* among multiple frames to visualize properly it’s performance

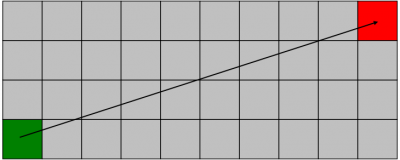
Straight line optimization

The idea is to check if the path can be done by just adding the initial and goal nodes. Such an approach will save us a quite high amount of computational time by not performing the algorithm directly.

As we were working on a 2D grid for this assignment, the task was really easy and fast. Just by checking if an obstacle lies inside the square that both nodes create is enough. The path will be a straight line if no obstacle is identified in such square.

Smoothing & Rubberbanding

Rubber banding removes inner paths that can be benefited with the straight line optimization while smoothing smooths the path of the agent by making use of the Catmull-Rom splines. As a result, the path the agent will follow is improved and sharp turns are avoided.

Heuristic functions

We took into account several heuristic cost functions to see their impact with the algorithm

Push start node onto the open list
    Compute total cost, f(x)

While the open list is not empty {
    Pop the cheapest node from the open list
    Check if the node is the goal node
        Done, we already get the node

    Erase the cheapest node from the open list
    Push it to the closed list

    For all neighboring slots {
        Get coordinates of the neighbor
        Check if the neighbor is valid
            Coordinate does not correspond to a wall, it is inside the grid and it is not inside the closed list

        Set the neighbor's g(x) cost to the cheapest's g(x) that we popped before
        
        If the neighbor is diagonal {
            Check if it is a valid diagonal
            Add sqrt(2) to the g(x) cost
        }

        If the neighbor is not diagonal
            Add 1 to the g(x) cost

        If the slot already exists in the open list {
            If the total cost of the current neighbor is cheaper {
                Update total cost (f(x)) of the node that is inside the open list
                Update the g(x) cost
            }
        }

        If the slot does not exist in the open list {
            Compute the heuristic cost to compute the total cost, f(x)
            Push neighbor to the open list
        }
    }
}